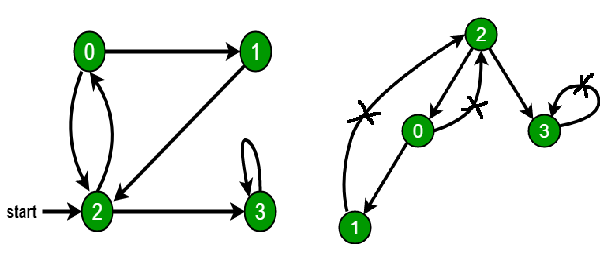
Depth First Traversal (or Search) for a graph is similar to Depth First Traversal of a tree. The only catch here is, unlike trees, graphs may contain cycles, so we may come to the same node again. To avoid processing a node more than once, we use a boolean visited array.
For example, in the following graph, we start traversal from vertex 2. When we come to vertex 0, we look for all adjacent vertices of it. 2 is also an adjacent vertex of 0. If we don’t mark visited vertices, then 2 will be processed again and it will become a non-terminating process. A Depth First Traversal of the following graph is 2, 0, 1, 3.
Implementation
# Python program to print DFS traversal from a
# given given graph
from collections import defaultdict
# This class represents a directed graph using adjacency list representation. Vertices are from 0 to n - 1
class Graph:
# Constructor
def __init__(self):
# default dictionary to store graph
self.graph = defaultdict(list)
# function to add an edge to graph
def addEdge(self, u, v):
self.graph[u].append(v)
# A function used by DFS
def DFSUtil(self, v, visited):
# Mark the current node as visited and print it
visited[v]= True
print v,
# Recur for all the vertices adjacent to this vertex
for i in self.graph[v]:
if visited[i] == False:
self.DFSUtil(i, visited)
# The function to do DFS traversal. It uses
# recursive DFSUtil()
def DFS(self, v):
# Mark all the vertices as not visited
visited = [False] * len(self.graph)
# Call the recursive helper function to print
# DFS traversal
self.DFSUtil(v, visited)
Kosaraju’s Two-Pass Algorithm for Strongly-Connected Components
- Run DFS on the graph with all edges reversed.
- Run DFS on the original graph.