Question

Given an Android 3x3 key lock screen and two integers m and n, where 1 ≤ m ≤ n ≤ 9, count the total number of unlock patterns of the Android lock screen, which consist of minimum of m keys and maximum n keys.

Rules for a valid pattern:

1. Each pattern must connect at least m keys and at most n keys.
2. All the keys must be distinct.
3. If the line connecting two consecutive keys in the pattern passes through any other keys, the other keys must have previously selected in the pattern. No jumps through non selected key is allowed.
4. The order of keys used matters.

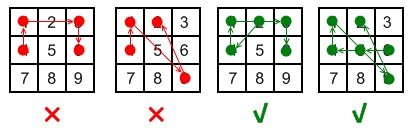
Explanation:

| 1 | 2 | 3 |
| 4 | 5 | 6 |
| 7 | 8 | 9 |

Invalid move: 4 - 1 - 3 - 6

Line 1 - 3 passes through key 2 which had not been selected in the pattern.

Invalid move: 4 - 1 - 9 - 2

Line 1 - 9 passes through key 5 which had not been selected in the pattern.

Valid move: 2 - 4 - 1 - 3 - 6

Line 1 - 3 is valid because it passes through key 2, which had been selected in the pattern

Valid move: 6 - 5 - 4 - 1 - 9 - 2

Line 1 - 9 is valid because it passes through key 5, which had been selected in the pattern.

Example:

Input: m = 1, n = 1
Output: 9

Solution

Use backtracking to remove invalid moves.

class Solution {
    private boolean[] used = new boolean[9];
    public int numberOfPatterns(int m, int n) {
        int res = 0;
        for (int i = m; i <= n; i++)
            res += calculatePatterns(-1, i);
        return res;
    }

    private boolean isValid(int last, int pos) {
        // first pos
        if(last == -1) return true;
        // horizontal, vertical neighbors and horse pattern
        else if (abs(pos - last) % 2 == 1) return true;
        // vertical two hops
        else if (abs(pos - last) == 6 && used[(pos + last) / 2]) return true;
        // horizontal two hops
        else if (abs(pos - last) == 2 && (pos + last) % 6 == 2 && used[(pos + last) / 2]) return true;
        // diagonal two hops
        else if (pos + last == 8 && pos % 2 == 0 && used[4]) return true;
        // diagonal one hop
        else if (abs(pos - last) == 4 && pos + last != 8) return true;
        else if (abs(pos - last) == 2 && (pos + last) % 6 != 2) return true;
        else return false;
    }

    private int calculatePatterns(int last, int remaining) {
        if (remaining == 0) return 1;
        int res = 0;
        for (int i = 0; i < 9; i++) {
            if (!used[i] && isValid(last, i)) {
                used[i] = true;
                res += calculatePatterns(i, remaining - 1);
                used[i] = false;
            }
        }
        return res;
    }

    private int abs(int a) {
        if(a >= 0) return a;
        else return -a;
    }
}